PR0 - Google's PageRank 0 Penalty
By the end of 2001, the Google search engine introduced a new kind of penalty for websites that use questionable search engine optimization tactics: A PageRank of 0. In search engine optimization forums it is called PR0 and this term shall also be used here. Characteristically for PR0 is that all or at least a lot of pages of a website show a PageRank of 0 in the Google Toolbar, even if they do have high quality inbound links. Those pages are not completely removed from the index but they are always at the end of search results and, thus, they are hardly to be found.
A PageRank of 0 does not always mean a penalty. Sometimes, websites which seam to be penalized simply lack inbound links with an sufficiently high PageRank. But if pages of a website which have formerly been placed well in search results, suddenly show the dreaded white PageRank bar, and if there have not been any substantial changes regarding the inbound links of that website, this means - according to the prevailing opinion - certainly a penalty by Google.
We can do nothing but speculate about the causes for PR0 because Google representatives rarely publish new information on Google's algorithms. But, non the less, we want to give a theoretical approach for the way PR0 may work because of its serious effects on search engine optimization.
The Background of PR0
Spam has always been one of the biggest problems that search engines had to deal with. When spam is detected by search engines, the usual proceeding is the banishment of those pages, websites, domains or even IP addresses from the index. But, removing websites manually from the index always means a large assignment of personnel. This causes costs and definitely runs contrary to Google's scalability goals. So, it appears to be necessary to filter spam automatically.
Filtering spam automatically carries the risk of penalizing innocent webmasters and, hence, the filters have to react rather sensibly on potential spam. But then, a lot of spam can pass the filters and some additional measures may be necessary. In order to filter spam effectively, it might be useful to take a look at links.
That Google uses link analysis in order to detect spam has been confirmed more or less clearly in WebmasterWorld's Google News Forum by a Google employee who posts as "GoogleGuy". Over and over again, he advises webmasters to avoid "linking to bad neighbourhoods". In the following, we want to specify the "linking to bad neighbourhoods" and, to become more precisely, we want to discuss how an identification of spam can be realized by the analysis of link structures. In particular, it shall be shown how entire networks of spam pages, which may even be located on a lot of different domains, can be detected.
BadRank as the Opposite of PageRank
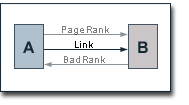
The theoretical approach for PR0 as it is presented here was initially brought up by Raph Levien (www.advogato.org/person/raph). We want to introduce a technique that - just like PageRank - analyzes link structures, but, that unlike PageRank does not determine the general importance of a web page but rather measures its negative characteristics. For the sake of simplicity this technique shall be called "BadRank".
BadRank is in priciple based on "linking to bad neighbourhoods". If one page links to another page with a high BadRank, the first page gets a high BadRank itself through this link. The similarities to PageRank are obvious. The difference is that BadRank is not based on the evaluation of inbound links of a web page but on its outbound links. In this sense, BadRank represents a reversion of PageRank. In a direct adaptation of the PageRank algorithm, BadRank would be given by the following formula:
BR(A) = E(A) (1-d) + d (BR(T1)/C(T1) + ... + BR(Tn)/C(Tn))
where
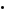 | BR(A) is the BadRank of page A, |
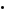 | BR(Ti) is the BadRank of pages Ti which are outbound links of page A, |
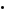 | C(Ti) is here the number of inbound links of page Ti and |
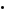 | d is the again necessary damping factor. |
In the previously discussed modifications of the PageRank algorithm, E(A) represented the special evaluation of certain web pages. Regarding the BadRank algorithm, this value reflects if a page was detected by a spam filter or not. Without the value E(A), the BadRank algorithm would be useless because it was nothing but another analysis of link structures which would not take any further criteria into account.
By means of the BadRank algorithm, first of all, spam pages can be evaluated. A filter assigns a numeric value E(A) to them, which can, for example, be based on the degree of spamming or maybe even better on their PageRank. Thereby, again, the sum of all E(A) has to equal the total number of web pages. In the course of an iterative computation, BadRank is not only transfered to pages which link to spam pages. In fact, BadRank is able to identify regions of the web where spam tends to occur relatively often, just as PageRank identifies regions of the web which are of general importance.
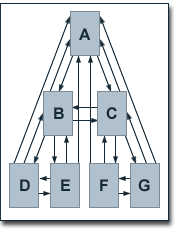
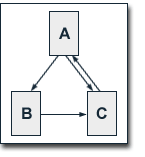
Of course, BadRank and PageRank have significant differences, especially, because of using outbound and inbound links, respectively. Our example shows a simple, hierarchically structured website that reflects common link structures pretty well. Each page links to every page which is on a higher hierachical level and on its branch of the website's tree structure. Each page links to pages which are arranged hierarchically directly below them and, additionally, pages on the same branch and the same hierarchical level link to each other.
The following table shows the distribution of inbound and outbound links for the hierarchical levels of such a site.
| Level | inbound Links | outbound Links |
| 0 | 6 | 2 |
| 1 | 4 | 4 |
| 2 | 2 | 3 |
As to be expected, regarding inbound links, a hierarchical gradation from the index page downwards takes place. In contrast, we find the highest number of outbound links on the website's mid-level. We can see similar results, when we add another level of pages to our website while the above described linking rules stay the same.
| Level | inbound Links | outbound Links |
| 0 | 14 | 2 |
| 1 | 8 | 4 |
| 2 | 4 | 5 |
| 3 | 2 | 4 |
Again, there is a concentration of outbound links on the website's mid-level. But most of all, the outbound links are much more evenly distributed than the inbound links.
If we assign a value of 100 to the index page's E(A) in our original example, while all other values E equal 1 and if the damping factor d is 0.85, we get the following BadRank values:
| Page | BadRank |
| A | 22.39 |
| B/C | 17.39 |
| D/E/F/G | 12.21 |
First of all, we see that the BadRank distributes from the index page among all other pages of the website. The combination of PageRank and BadRank will be discussed in detail below, but, no matter how the combination will be realized, it is obvious that both can neutralize each other very well. After all, we can assume that also the page's PageRank decreases, the lower the hierarchy level is, so that a PR0 can easily be achieved for all pages.
If we now assume that the hierarchically inferior page G links to a page X with a constant BadRank BR(X)=10, whereby the link from page G is the only inbound link for page X, and if all values E for our example website equal 1, we get, at a damping factor d of 0.85, the following values:
| Page | BadRank |
| A | 4.82 |
| B | 7.50 |
| C | 14.50 |
| D | 4.22 |
| E | 4.22 |
| F | 11.22 |
| G | 17.18 |
In this case, we see that the distribution of the BadRank is less homogeneous than in the first scenario. Non the less, a distribution of BadRank among all pages of the website takes place. Indeed, the relatively low BadRank of the index page A is remarkable. It could be a problem to neutralize its PageRank which should be higher compared to the rest of the pages. This effect is not really desirable but it reflects the experiences of numerous webmasters. Quite often, we can see the phenomenom that all pages except for the index page of a website show a PR0 in the Google Toolbar, whereby the index page often has a Toolbar PageRank between 2 and 4. Therefore, we can probably assume that this special variant of PR0 is not caused by the detection of the according website by a spam filter, but the site rather received a penalty for "linking to bad neighbourhoods". Indeed, it is also possible that this variant of PR0 occurs when only hierarchical inferior pages of a website get trapped in a spam filter.
The Combination of PageRank and BadRank to PR0
If we assume that BadRank exists in the form presented here, there is now the question in which way BadRank and PageRank can be combined, in order to penalize as much spammers as possible while at the same time penalizing as few innocent webmasters as possible.
Intuitively, implementing BadRank directly in the actual PageRank computations seems to make sense. For instance, it is possible to calculate BadRank first and, then, divide a page's PageRank through its BadRank each time in the course of the iterative calculation of PageRank. This would have the advantage, that a page with a high BadRank could pass on just a little PageRank or none at all to the pages it links to. After all, one can argue that if one page links to a suspect page, all the other links on that page may also be suspect.
Indeed, such a direct connection between PageRank and BadRank is very risky. Most of all, the actual influence of BadRank on PageRank cannot be estimated in advance. It is to be considered that we would create a lot of pages which cannot pass on PageRank to the pages they link to. In fact, these pages are dangling links, and as it has been discussed in the section on outbound links, it is absolutely necessary to avoid dangling links while computing PageRank.
So, it would be advisable to have separate iterative calculations for PageRank and BadRank. Combining them afterwards can, for instance, be based on simple arithmetical operations. In principle, a subtraction would have the desirable consequence that relatively small BadRank values can hardly have a large influence on relatively high PageRank values. But, there would certainly be a problem to achieve PR0 for a large number of pages by using the subtraction. We would rather see a PageRank devaluation for many pages.
Achieving the effects that we know as PR0 seems easier to be realized by dividing PageRank through BadRank. But this would imply that BadRank receives an extremely high importance. However, since the average BadRank equals 1, a big part of BadRank values is smaller than 1 and, so, a normalization is necessary. Probably, normalizing and scaling BadRank to values between 0 and 1 so that "good" pages have values close to 1, and "bad" pages have values close to 0 and, subsequently, multiplying these values with PageRank would supply the best results.
A very effective and easy to realize alternative would probably be a simple stepped evaluation of PageRank and BadRank. It would be reasonable that if BadRank exceeds a certain value it will always lead to a PR0. The same could happen when the relation of PageRank to BadRank is below a certain value. Additionally, it would make sense that if BadRank and/or the relation of BadRank to PageRank is below a certain value, BadRank takes no influence at all.
Only if none of these cases occurs, an actual combination of PageRank and BadRank - for instance by dividing PageRank through BadRank - would be necessary. In this way, all unwanted effects could be avoided.
A Critical View on BadRank and PR0
How Google would realize the combination of PageRank and BadRank is of rather minor importance. Indeed, a separate computation and a subsequent combination of both has the consequence that it may not be possible to see the actual effect of a high BadRank by looking at the Toolbar. If a page has a high PageRank in the original sense, the influence of its BadRank can be negligible. But if another page links to it, this could have quite serious consequences.
An even bigger problem is the direct reversion of the PageRank algorithm as we have presented it here: Just as an additional inbound for one page can do nothing but increasing this page's PageRank, an additional outbound link can only increase its BadRank. This is because of the addition of BadRank values in the BadRank formula. So, it does not matter how many "good" outbound links a page has - one link to a spam page can be enough to lead to a PR0.
Indeed, this problem may appear in exceptional cases only. By our direct reversion of the PageRank algorithm, the BadRank of a page is divided by its inbound links and single links to pages with high BadRank transfer only a part of that BadRank in each case. Google's Matt Cutts' remark on this issue is: "If someone accidentally does a link to a bad site, that may not hurt them, but if they do twenty, that's a problem." (searchenginewatch.com/sereport/02/11-searchking.html)
However, as long as all links are weighted uniformly within the BadRank computation, there is another problem. If two pages differ widely in PageRank and both have a link to the same page with a high BadRank, this may lead to the page with the higher PageRank suffering far less from the transferred BadRank than the page with the low PageRank. We have to hope that Google knows how to deal with such problems. Nevertheless it shall be noted that, regarding the procedure presented here, outbound links can do nothing but harm.
Of course, all statements regarding how PR0 works are pure speculation. But in principle, the analysis of link structures similarly to the PageRank technique should be the way how only Google understands to deal with spam.
PageRank and Google are trademarks of Google Inc., Mountain View CA, USA. PageRank is protected by US Patent 6,285,999.
The content of this document may be reproduced on the web provided that a copyright notice is included and that there is a straight HTML hyperlink to the corresponding page at
pr.efactory.de in direct context.